Rational Chart Making

Oftentimes a question will ask for intervals of increasing and decreasing intervals. What it asks for is a chart. In this chart you will have included:

• Critical Values The boilerplate chart looks as such:

Interval	x < ?	? < x < ?	? < x < ?	…	? < x
f(x)	+/-	+/-	+/-		+/-
slope	+/-	+/-	+/-		+/-
change in slope	+/-	+/-	+/-		+/-

We don’t make x = anything. Because you cannot have a change in slope at one point.

f(x)

SImply see if the function is above the x-axis or not

Slope

Negative slope looks like this: Positive slope looks like this:

Change In Slope

A smiley is positive A frown is negative

Example

So we may have a reciprocal function with the equation: $y=\frac{2x-5}{x+2}$ We need to find the Critical Points and the X Intercept

X intercept

$0=\frac{2x-5}{x+2}$ $2x-5=0$ $x=5/2$

Critical Points

$undef=\frac{2x-5}{x+2}$ $0=x+2$ $x=-2$

Before we Chart, we must graph it

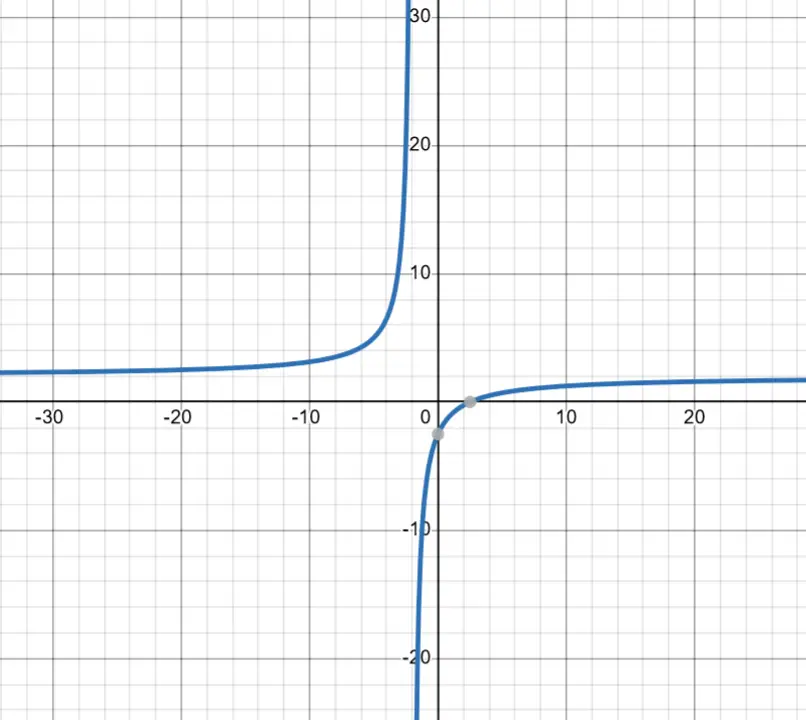
Charting

Our points are 5/2 and -2

Interval	x < -2	-2 < x < 2.5	x > 2.5
f(x)	+	-	+
slope	+	+	+
change in slope	+	-	-