Weight Balance Tree Rebalance

Case 1 - Right Heavy Tree

Assuming:

• WBT is right-heavy ($\text{weight}(v.\text{right})>\text{weight}(v.\text{left})\times 3$)
• $\text{weight(v.right.left)}<\text{weight(v.right.right)}\times 2$ balance by single counter-clockwise rotation.

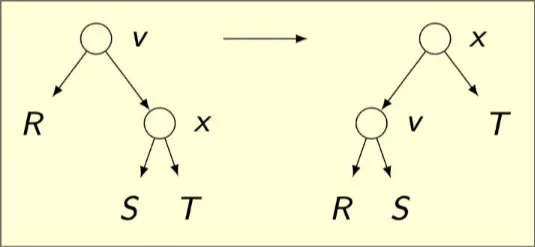
Proof - Uses Diagram Above

1. Let $r=\text{size}(v.left)$
2. Let $s=\text{size}(v.right.left)$
3. Let $t=\text{size}(v.right.right)$
4. Suppose $s+1<2(t+1)$
5. Suppose $3(r+1)<s+t+2$
6. Consider cases:
   1. Case 1: node added to $v.right$ to cause imbalance
      1. Suppose before addition, we had a WBT $v$
      2. This means, $\frac{1}{3}\ast \text{weight}(v.right)\le \text{weight}(v.left)\le 3\ast \text{weight}(v.right)$
      3. $⟹\frac{1}{3}(s+t+1)\le r+1\le 3(s+t+1)$
      4. Suppose before addition, we had a WBT $x$
      5. This means, $\frac{1}{3}\ast \text{weight}(x.right)\le \text{weight}(x.left)\le 3\ast \text{weight}(x.right)$
      6. $⟹\frac{1}{3}(t)\le s+1\le 3(t)$
      7. WTS: after addition, and rotation, we have a WBT $v$ and WBT $x$
      8. In other words, WTS:
         1. $\frac{1}{3}(r+s+2)\le t+1\le 3(r+s+2)$ (WBT x)
         2. $\frac{1}{3}(s+1)\le r+1\le 3(s+1)$ (WBT v)
      9. $3(r+1)<s+t+2=(s+1)+(t+1)<2(t+1)+(t+1)=3(t+1)$ by 4,5
      10. $⟹r<t$
      11. Then, $r+s+2=(r+1)+(s+1)<(t+1)+(s+1)<(t+1)+2(t+1)=3(t+1)$ by 4, 10
      12. $t+1\le 3(s+1)+1\le 3(r+s+2)$ by 8.1
      13. $r+1<t+1\le 3(s+1)+1$, therefore $r+1\le 3(s+1)$
      14. Note that $s+1\le s+t+1\le 3(r+1)⟹\frac{1}{3}(s+1)\le r+1$
      15. Thus, we have shown all cases
   2. Case 2: node removed from $v.left$ to cause imbalance
      1. Suppose before removal, we had a WBT $v$
      2. This means, $\frac{1}{3}\ast \text{weight}(v.right)\le \text{weight}(v.left)\le 3\ast \text{weight}(v.right)$
      3. $⟹\frac{1}{3}(s+t+2)\le r+2\le 3(s+t+2)$
      4. Suppose before addition, we had a WBT $x$
      5. This means, $\frac{1}{3}\ast \text{weight}(x.right)\le \text{weight}(x.left)\le 3\ast \text{weight}(x.right)$
      6. $⟹\frac{1}{3}(t+1)\le s+1\le 3(t+1)$
      7. WTS: after removal, and rotation, we have a WBT $v$ and WBT $x$
      8. In other words, WTS:
         1. $\frac{1}{3}(t+1)\le r+s+2\le 3(t+1)$ (WBT x)
         2. $\frac{1}{3}(r+1)\le s+1\le 3(r+1)$ (WBT $v$)
      9. $3(r+1)<s+t+2=(s+1)+(t+1)<2(t+1)+(t+1)=3(t+1)$ by 4,5
      10. $⟹r<t$
      11. $r+s+2=(r+1)+(s+1)<(t+1)+(s+1)<(t+1)+2(t+1)=3(t+1)$ by 4, 11
      12. $t+1\le 3(s+1)\le 3(r+s+2)$ by 8.1
      13. $r+1<t+1\le 3(s+1)$ by 8.1, 10
      14. $s+1\le 3(r+2)-t-1=3(r+1)+2-t\le 3(r+1)$ when $t\ge 2$

Case 2 - Left Heavy Tree

When the WBT is left-heavy - single counter-clockwise rotation.