Limit Existence

Existence Hints

A limit exists if:

• A valid coordinate exists
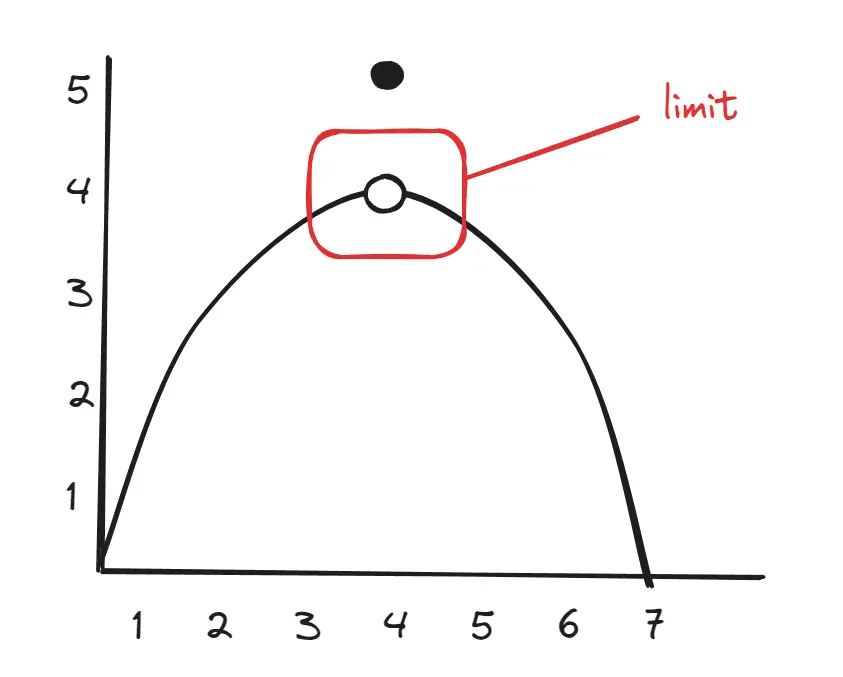
• A valid hole coordinate exists. Limits exist at holes They do not exist if:
• Single limits ${\lim }_{x\to a^{-}}\ne {\lim }_{x\to a^{+}}$
  • There is a asymptote at the x value with No cross over point
• Algebra with Limit Properties returns undefined
• They approach infinity
• The value that approach is oscillating between two values (https://www.youtube.com/watch?v=isMZo-OFJOs)
  • ${\lim }_{x\to \infty }\sin x$
  • ${\lim }_{x\to -\infty }\sin x$
  • ${\lim }_{x\to \infty }\cos x$
  • ${\lim }_{x\to -\infty }\cos x$
  • ${\lim }_{x\to -\infty }\tan x$
  • ${\lim }_{x\to -\infty }\tan x$
  • ${\lim }_{x\to \infty }\frac{1}{\sin x}$
  • ${\lim }_{x\to -\infty }\frac{1}{\sin x}$
  • ${\lim }_{x\to \infty }\frac{1}{\cos x}$
  • ${\lim }_{x\to -\infty }\frac{1}{\cos x}$
  • ${\lim }_{x\to \infty }\frac{1}{\tan x}$
  • ${\lim }_{x\to -\infty }\frac{1}{\tan x}$

Paths Definition

A limit exists if it takes the same value from all Paths

Algebraic Proof

• Use Algebra with Limit Properties
• You can use direct substitution if there is no hole in the equation

Limit Finding Techniques

• Limit Rationalization
• Limit Substitution
• Limit Division
• Limits with Euler’s Number
• Squeeze Theorem
• L’Hopital’s Rule
• Limits Using Polar Coordinates

Graphic Proof

• The limit is that point it naturally approaches. Follow the curve, not the jump