Pumping Lemma

Used to prove a language is not regular.

Lemma

• Given $L$ as a Regular Language
• $\forall$ String $s\in L$, $\exists$ $s^{\prime }$ comprised of $s$ and a subsequence in $s$ that can be repeated/pumped forever s.t $s^{\prime }\in L$

Alternative Lemma

1. If $L$ is a Regular Language
2. Then, there is an integer $n>0$ with the property that: $(\ast )$ for any stirng $x\in L$ where $|x|\ge n$, there are strings $u,v,w$ s.t:
   1. $x=uvw$
   2. $v\ne ϵ$
   3. $|uv|\le n$
   4. $u{v}^{k}w\in L,\forall k\in \mathbb{N}$

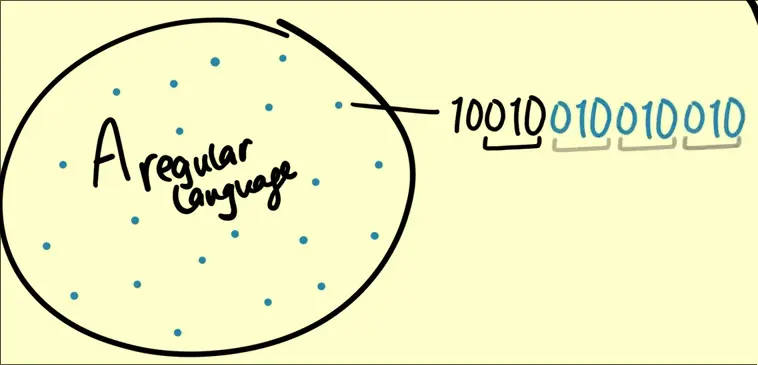
Intuition

Any string of atleast length $n$ has a substring that can be repeated an infinite number of times and still be in the language

Disproof Structure

1. Suppose $L$ is Regular Language
2. Since $L$ is regular, we apply Pumping Lemma and assert there is a $n>0$ that satisfies $(\ast )$
3. Give a particular string $x$ s.t
   1. $x\in L$
   2. $|x|>n$
4. By pumping lemma, there are strings $u,v,w$. Pick specific $k\in \mathbb{N}$ s.t $u{v}^{k}w\notin L$
5. Then, we have proved that this language is not regular.

Examples

• Pumping Lemma Disproving Regular Language Example

Proof of P.L

1. Suppose $L$ is regular
2. Then, let $M$ be a DFSA s.t $\mathcal{L}(M)=L$ by The Big Result
3. Let $n$ be the number of states in $M$
4. Then, $x=a_1{a}_2,\dots ,a_n$
5. The states include $q_0,q_1,q_2,..,q_n$
6. $q_i={\delta }^{\ast }(s_1,x[:i])$ This is the state you get to after reading the first $i$ symbols.
7. Denote $u=a_1{a}_2\dots a_i$
8. Denote $v=a_{i+1}\dots a_j$
9. Denote $w=a_{j+1}\dots a_n$
10. Then, $a_{|x|}\in L$
11. Then $q_{|x|}\in F$
12. Then, we get that every repeated $v$ allows $uvw$ to be in the language