Maximum Likelihood Estimator

Estimator to find the most likely distribution a Statistic came from via a Likelihood Function

Motivation

• With two distributions $P_1,P_2$ as Uniform Discrete Probability Distribution
• Under $P_1$, $X\sim \text{Uniform}(1,2,\dots ,10^3)$
• Under $P_2$, $X\sim \text{Uniform}(1,2,\dots ,10^6)$
• We observe one sample value of $X$ - say 10
• Which distribution did it come from?
• Which distribution is it more likely to have produced this random number

Theorem

The likelihood that a Parameter came from a distribution is the distribution that has the highest likelihood value at the Likelihood Function at the given statistic.

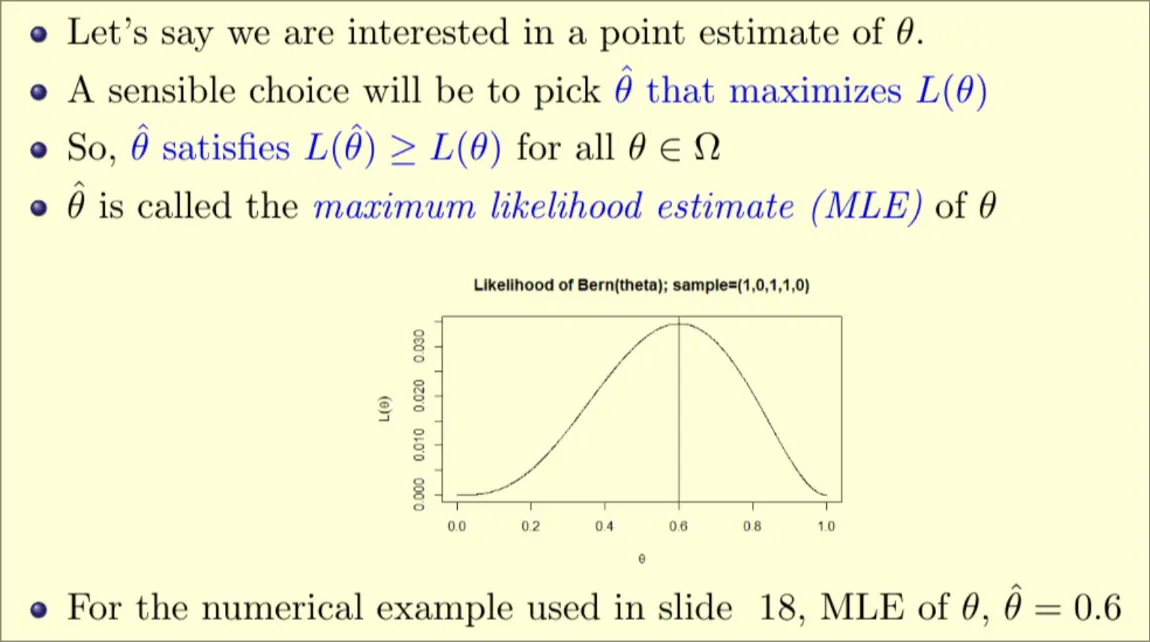
Properties

• MLE is not unique
• MLE may not exist
• Likelihood may not always be differentiable
  • Example: $X_1,\dots ,X_n{\sim }_{iid}\text{Uniform}(0,\theta )$, in this case, $\hat{\theta }=max(x_1,\dots ,x_n)$
  • We have to be careful when range of $X$ involves Parameter $\theta$
• Invariance Property of MLE

Computation of MLE

• Likelihood Function
• Log-Likelihood Function

Computation/Differentiation Technique Example

Solve equation $\frac{\partial l(\theta )}{\partial \theta }$ for $X_1,\dots ,X_n{\sim }^{iid}\text{Poisson}(\lambda )$. $P[X=x]=\frac{e^{-\lambda }{\lambda }^x}{x!}$ Then, $L(\lambda )=P[X_1=x_1]\times P[X_2=x_2]\times \cdots \times P[X_n=x_n]$ $=\frac{e^{-\lambda }{\lambda }^{x_1}}{x_1!}\ast \cdots \ast \frac{e^{-\lambda }{\lambda }^{x_n}}{x_n!}$ $=\frac{e^{-n\lambda }{\lambda }^{{\sum }_{i=1}^n{x}_i}}{{\Pi }_{i=1}^n{x}_1!}$

Finding MLE Analytically Example

For $X_1,\dots ,X_n\sim \text{Uniform}(0,\theta )$ $f(x)=\frac{1}{\theta }$ Then, $L(\theta )={\frac{1}{\theta }}^n$ To maximize $L(\theta )$, we minimize $\theta$ So, $\theta$ is the smallest value you see in the sample statistics.